R-quadrado ajustado: definição, como interpretar e exemplos

O  R-quadrado ajustado ou R² modificado determina a extensão da variância da variável dependente que pode ser explicada pela variável independente. A especialidade de R² ajustado é que não tem em conta o impacto de todas as variáveis independentes, mas apenas aquelas que têm impacto na variação da variável dependente. O valor de R² ajustado também pode ser negativo, embora não seja negativo a maior parte do tempo.

O que é o R-quadrado ajustado?

Fórmula do R-quadrado ajustado

A fórmula para calcular o R²  ajustado é mostrada abaixo:

R²= {(1 / N) * Σ [(xi – x) * (yi – y)] / (σx * σy)} ^ 2

• R² = R quadrado ajustado da equação de regressão
• N = Número de observações na equação de regressão
• Xi = variável independente da equação de regressão
• X = Média da variável independente da equação de regressão
• Yi = variável dependente da equação de regressão
• Y = Média da variável dependente da equação de regressão
• σx = Desvio padrão da variável independente
• σy = Desvio padrão da variável dependente

Leia ainda 👉 Desvio padrão: o que é?

Interpretação de R-quadrado ajustado

R² ajustado, determina a extensão da variância da variável dependente que pode ser explicada pela variável separada. Ao observar o valor ajustado de R², pode avaliar-se se os dados da equação de regressão estão a ser correctamente ajustados. Quanto maior R² ajustado, melhor é a equação de regressão, uma vez que implica que a variável independente escolhida para determinar a variável dependente pode explicar a variação na variável dependente.

Da mesma forma, as sociedades só valorizam aquilo que medem. Por exemplo, os países nórdicos ocupam um lugar de destaque no Relatório Global sobre a Competitividade do Fórum Económico Mundial. Os seus orçamentos concentram-se nos motores do crescimento económico. Estes são educação de classe mundial, programas sociais e um elevado nível de vida. Estes factores criam uma mão-de-obra qualificada e motivada. Estes países têm também taxas de impostos elevadas. Isto trava o crescimento do PIB. Mas eles utilizam os rendimentos para investir nos blocos de construção do crescimento económico a longo prazo.

Ejemplos de fórmula  (con plantilla de Excel)

Exemplo 1

Vamos tentar compreender o conceito de R² ajustado com a ajuda de um exemplo. Vamos tentar descobrir qual é a relação entre a distância percorrida pelo condutor do camião e a idade do condutor do camião. Alguém faz uma equação de regressão para validar se o que pensa sobre a relação entre duas variáveis é também validado pela equação de regressão.

Neste exemplo em particular, veremos qual é a variável dependente e qual é a variável independente. A variável dependente nesta equação de regressão é a distância percorrida pelo camionista e a variável independente é a idade do camionista.

Ao executar uma regressão com as variáveis, obtivemos o quadrado R² ajustado para que seja 65%. A próxima imagem mostra a saída de regressão para as variáveis. O conjunto de dados e variáveis são apresentados na folha de Excel em anexo.

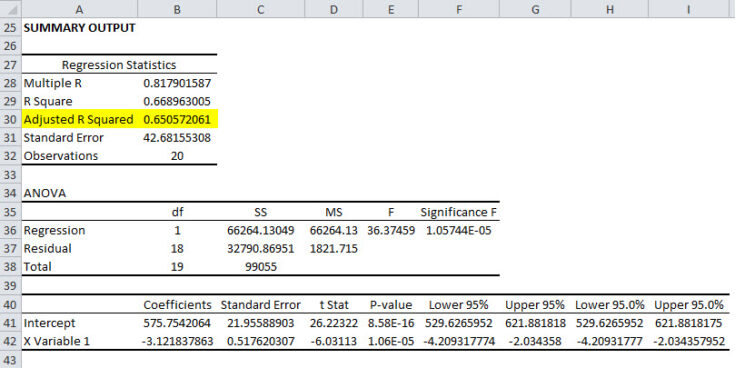
O valor R² ajustado de 65% para esta regressão implica que 65% da variação da variável dependente é explicada pela variável independente. Idealmente, um investigador procurará o coeficiente de determinação mais próximo dos 100%.

Exemplo 2

Vamos tentar compreender o conceito de quadrado R ajustado com a ajuda de outro exemplo. Vamos tentar descobrir qual é a relação entre a altura dos alunos de uma turma e a média das notas desses alunos. Neste exemplo em particular, veremos qual é a variável dependente e qual é a variável independente. A variável dependente nesta equação de regressão é o GPA dos estudantes e a variável independente é a altura dos estudantes.

Executando uma regressão com as variáveis obtemos que o R² ajustado seja insignificante ou negativo. A próxima imagen mostra a saída de regressão para as variáveis. O conjunto de dados e variáveis são apresentados na folha Excel em anexo.

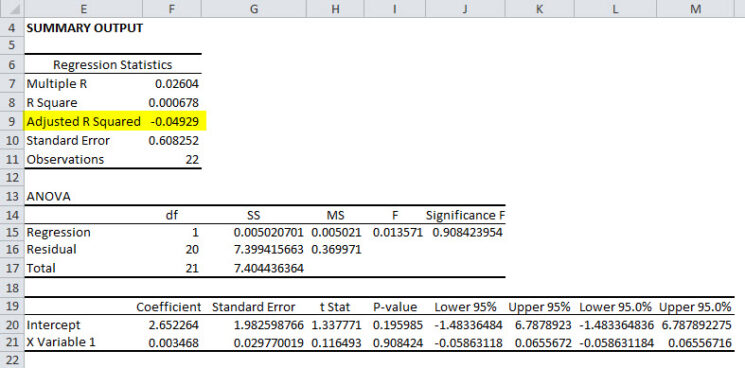
O valor R² ajustado é insignificante para esta regressão, o que implica que a variação na variável dependente não é explicada pela variável independente. Idealmente, um investigador procurará o coeficiente de determinação mais próximo dos 100%.

Interpretação

O quadrado R ajustado é um resultado muito importante para saber se o conjunto de dados é adequado ou não. Alguém faz uma equação de regressão para validar se o que pensa sobre a relação entre duas variáveis é também validado pela equação de regressão. Quanto maior for o R² ajustado, melhor é a equação de regressão, uma vez que implica que a variável independente escolhida para determinar a variável dependente seja correctamente escolhida. Idealmente, um investigador procurará o coeficiente de determinação mais próximo dos 100%.