Leonardo Fibonacci di Pisa – Biografia
Leonardo Fibonacci di Pisa, mais reconhecido como Fibonacci (que significa filho de Bonacci), nasceu na cidade italiana de Pisa e viveu de 1170 a 1250. Chamou-se a si mesmo “Bigollo”, que significa “bom para nada”. Foi no meio desta actividade comercial que Leonardo da Pisa começou a formar como comerciante e matemático na cidade de Bugia, hoje Bejaia um porto no nordeste da Argélia.
Biografia de Leonardo Fibonacci di Pisa

Muito pouco se sabe sobre a vida de Leonardo Fibonacci; no entanto, no prefácio de um dos seus livros mais importantes, o Liber Abaci, Leonardo comenta que foi o seu pai que lhe ensinou Aritmética e o encorajou a estudar Matemática. Em Bugia Leonardo recebeu este tipo de ensino de professores árabes, o que foi sem dúvida a melhor coisa que podia acontecer a um jovem italiano medieval.
Tornou-se especialista em Aritmética e nos diferentes sistemas de numeração que eram utilizados na altura. Logo se convenceu de que o sistema hindu-arábico era superior a qualquer dos utilizados nos diferentes países que tinha visitado. Decidiu levar este sistema para Itália e para toda a Europa, se possível, onde ainda se usavam os numerais romanos e o ábaco. O estudo da matemática e formas mais práticas de a aplicar como um instrumento indispensável para o desenvolvimento do comércio ocupou-o praticamente toda a sua vida.
Leonardo Fibonacci regressou a Pisa por volta de 1200 e lá escreveu muitos livros e textos sobre matemática. Na época em que viveu ainda não existia a gráfica, por isso os seus livros eram escritos à mão e as cópias dos mesmos que circulavam eram também feitas à mão. É fácil imaginar a pequena quantidade de cópias que poderia circular naquela altura e embora pareça impossível ainda hoje, foram preservadas cópias dos seguintes livros: “Liber Abaci”, escrito em 1202; “Practica geometriae”, escrito em 1220; “Flos”, escrito em 1225 e “Liber quadratorum”, escrito em 1227. No entanto, muitos mais se perderam no decurso da história.
No ano 1200, Fibonacci publicou o seu famoso Liber Abacci, onde mencionou (e serviu para introduzir na Europa) uma das ferramentas matemáticas mais importantes da história: o sistema decimal.
A reputação de Leonardo cresceu a tal ponto que em 1225 foi reconhecido como um dos melhores matemáticos,, vários tribunais e lojas pediam-lhe conselhos.
A sucessão de Fibonacci
A sequência de Fibonacci, incluída na obra de Leonardo de Pisa, Liber Abacci, coloca o problema de calcular o crescimento de uma população de coelhos desde o início. Para o efeito, propõe a seguinte solução:
Começa com um par de coelhos que estão em idade fértil durante um mês. Assume-se que em cada ciclo de um casal fértil nasce exactamente um novo par de coelhos, que novamente estão durante um mês em idade fértil. Sob estes pressupostos, ele resolve o problema introduzindo uma recorrência que o matemático francês Edouard Lucas do S.XIX, batizou como a Sucessão Fibonacci em sua honra. É apresentado como uma solução para um problema matemático que se refere à taxa de reprodução dos coelhos em determinadas circunstâncias.
A sequência ou série de Fibonacci é calculada adicionando ao número atual o número anterior, de modo a que: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,…
Propriedades da sucessão de Fibonacci
- Cada número da sequência de Fibonacci é composto pela soma dos dois números anteriores; a sequência de Fibonacci começa com uma repetição do número 1. Em símbolos, pode ser escrito da seguinte forma: tn = tn-1 + tn-2
- A relação entre um número e o seu antecessor (tn/tn-1) tende a Phi= (1+ 5^(1/2))/ 2 ≅ 1,618, enquanto a relação entre um número e o seu predecessor (tn-1/tn), tendem a 0,618 (o inverso de Phi). Estas relações são quebradas apenas nos três primeiros números da série, enquanto se torna mais evidente à medida que os valores são maiores. O resultado dos quocientes entre os números oscilam alternadamente em torno destes valores, estando cada vez mais próximos deles.
- As relações entre números alternados (tn/tn-2 ou tn-2/tn) são próximas de 2618 ou o seu inverso, 0,382, respectivamente.
- A soma dos dez primeiros termos da sequência é igual a onze vezes o seu sétimo termo (isto cumpre-se para qualquer sequência construída como a de Fibonacci, sem importar quais sejam os dois números iniciais).
- Se toma um número qualquer da sequência a partir do 3, multiplica-se por 4 e se acrescenta o número correspondente a três termos anteriores, obtém-se o número da sequência três lugares mais adiante. Algébrica: tn*4 + tn-3= tn+3. Por exemplo: 21*4+5 = 89 (lembrando que a série é: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89)
Fibonacci na análise técnica
A sequência de Fibonacci é largamente utilizada na análise técnica, e dela derivam várias ferramentas, que veremos a seguir. Estas ferramentas utilizam o quociente entre os diferentes dígitos da série, principalmente entre um número e o anterior, quanto mais alto estes forem, o resultado se aproxima mais do número áureo, este número é 1618. A equação básica do número Aureo é:
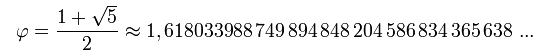
A partir do número áureo 1.618, aparecem uma série de proporções que matematicamente têm uma relação direta com este dígito e que podemos usar na análise técnica quando analisamos os gráficos:
| Principais proporções |
| 0,236 |
| 0,328 |
| 0,5 |
| 0,618 |
| 0,746 |
| 1 |
| 1,382 |
| 1,618 |
| 2,618 |
| 4,618 |
Análise técnica de ferramentas Fibonacci
Medidas temporárias de Fibonacci. As zonas temporais de Fibonacci são utilizadas contando para a frente a partir de um ponto significativo de máximos ou mínimos, é perfurado e arrastado até ao seguinte máximo ou mínimo significativo. As linhas marcadas no gráfico são interpretadas como importantes pontos de viragem no futuro. Num gráfico diário, o analista conta para a frente o número de dias de negociação Fibonacci, ou seja, os dias número 5, 8, 13, 21, 34, etc. De qualquer modo, não há necessidade de contar os dias, já que ao aplicar a ferramenta, as linhas temporais aparecem automaticamente no gráfico. A utilização desta técnica é menos aconselhável em gráficos de tempo mais curtos.
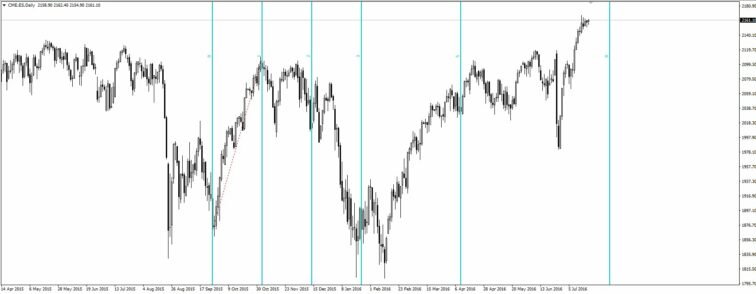
Abanicos Fibonacci. São muito fáceis de usar. O que esta ferramenta nos diz é o tempo e a profundidade da correcção da onda que irá seguir o impulso. Para tal, traça-se uma linha do mínimo até ao máximo do impulso. A seguir encontra-se na parte inferior uma série de linhas com diferentes ângulos de inclinação diretamente relacionados com as proporções angulares Fibonacci mais importantes. Esta ferramenta tem de ser traçada de mínimo a máximo se o impulso principal for de alta e do máximo para o mínimo se o impulso principal for de baixa.
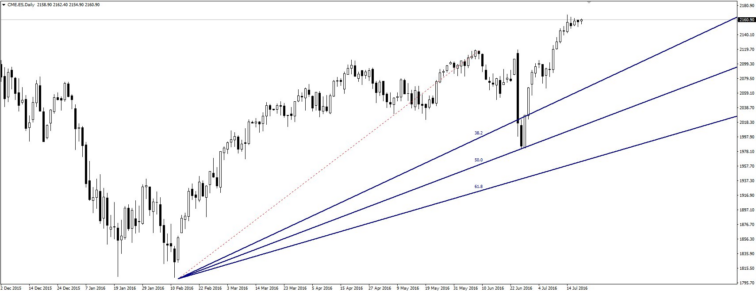
Expansão Fibonacci. Para traçar esta ferramenta vamos precisar de um primeiro impulso e de um movimento corretivo, ao contrário de outras ferramentas. A expansão Fibonacci permite-nos projectar o potencial da ascensão para saber até onde pode continuar o impulso. É usado antes de terminar a correcção. O cursor é levado para a base do impulso, e levado ao máximo da primeira sub onda interna, logo se volta a levar até a base da segunda sub onda interna. Então, dependendo das diferentes linhas de relação Fibonacci, pode-se ver até onde o impulso pode chegar.
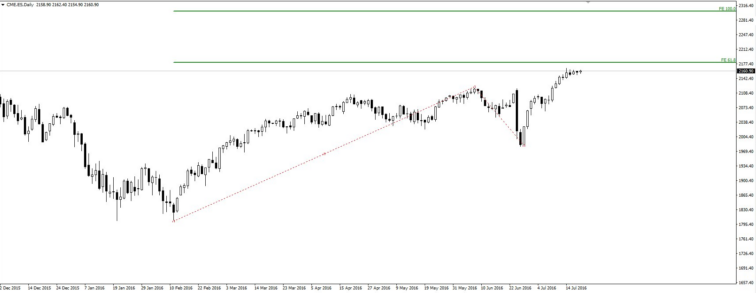
Retrações de Fibonacci. Os recuos de Fibonacci podem ser a ferramenta mais utilizada derivada desta série numérica. Esta ferramenta é usada para identificar as áreas onde um movimento correctivo pode ser interrompido, por isso, para usá-lo previamente, precisamos de um movimento impulsivo que já tenha terminado, caso contrário a ferramenta não funcionará. Para utilizar correctamente a ferramenta, devemos tomar o mínimo e o máximo do impulso, e com estes pontos vamos traçar o impulso, automaticamente nos devolverá os níveis derivados desta sucessão de números. Por defeito, os níveis indicados são 23,6%, 38,2%, 50% e 61,8%, sendo este último o equivalente ao número áureo, segundo a teoria, a zona mais provável na que pode terminar o processo correctivo da tendência é entre 50% e 61,8%.
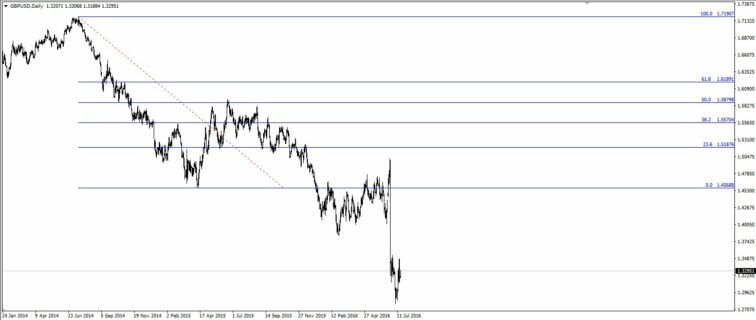
Na imagem acima podemos ver como o preço terminou o seu processo corretivo (neste caso em alta, porque o principal impulso foi para baixo) ao nível de 50% e continuou com a tendência principal, para baixo.
