Equação de Fisher: descubra o que é
A “equação de Fisher” é utilizada principalmente no setor financeiro para calcular os rendimentos dos títulos ou as taxas de retorno dos investimentos. Da mesma forma, a equação de Fisher é utilizada em situações onde os investidores exigem uma recompensa adicional para compensar as perdas no poder de compra devido à alta inflação.
O que é a equação de Fisher?
A equação de Fisher, que deve o seu nome ao economista estadunidense Irving Fisher, é uma equação utilizada na teoria económica que relaciona as taxas de juro com a taxa de inflação. Mais especificamente, a equação de Fisher estabelece, através da igualdade, a forma como a taxa de juro, tanto nominal como real, está relacionada com a inflação prevista. A equação é a seguinte:
Taxa nominal= Taxa de juro real + taxa de inflação esperada
Por outras palavras, a equação de Fisher conclui que, para determinar a taxa de juro real de um empréstimo (por exemplo) será necessário descontar a taxa de inflação esperada à taxa de juro nominal esperada. Por exemplo: se os credores exigirem uma taxa de juro real de 3%, mas, simultaneamente, se esperar uma inflação de 2%, nessa situação e de acordo com a equação de Fisher, a taxa de juro nominal será de 5%.
Da análise desta equação emerge o chamado Efeito Fisher: os aumentos na taxa de inflação são transmitidos, um a um, à taxa de juro nominal.
Qual é a diferença entre a taxa de juro real e nominal?
Para compreender completamente a equação de Fisher, é necessário fazer uma breve descrição de ambas as taxas de juro. A taxa de juro nominal é a que mostra o rendimento de uma operação como a diferença entre dois preços, enquanto a taxa de juro real tem em conta a possível alteração do poder de compra do dinheiro, ou seja, tem em conta a inflação. Portanto, na equação de Fisher, a taxa de juro nominal inclui, ou ainda não foi descontada, a taxa de inflação, enquanto se eliminarmos a taxa de juro real a igualdade será o resultado de subtrair ao nominal a taxa de inflação.
Leia também 👉 Juros simples e compostos: o que são e como usá-los
Por que razão a equação de Fisher é útil para explicar as taxas de juro?
Se olharmos para as tendências das taxas de inflação dos últimos anos, podemos concluir que a equação de Fisher é cumprida porque as evoluções destes dois dados andaram de mãos dadas, ou seja, quando a inflação é alta, as taxas de juro nominais tendem a ser altas e quando é baixa, tendem a ser baixas.
Esta estreita relação entre as duas taxas pode ser verificada em diferentes países, dando mais argumentos à afirmação de que a equação é uma fórmula a ter em conta se queremos prever adequadamente o comportamento das taxas de juro. No gráfico seguinte podemos ver para o caso dos EUA, com dados aproximados, a tendência que têm seguido e como estão estreitamente relacionados:
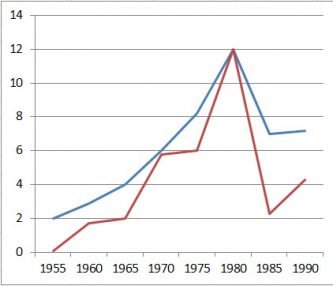
– Taxa de juros nominal (azul)
– Taxa de inflação (vermelho)
Além disso, a equação de Fisher é apreciada por muitos investidores da bolsa, uma vez que os preços das obrigações variam inversamente com as taxas de juro, pelo que se previrmos adequadamente os movimentos das taxas de juro, os nossos retornos de investimento em ações podem aumentar. Um exemplo disso é que empresas de Wall Street contratam profissionais para vigiar os movimentos de políticas monetárias e inflação, de modo a prever melhor as taxas de juro.
Compreender a equação de Fisher
Para entender melhor a equação de Fisher, podemos observar dois exemplos. Primeiro, uma pessoa que pede um empréstimo. Utilizaremos uma situação irrealista, de forma a simplificar a análise. Suponhamos que Matías pede um empréstimo de 1.000 euros e com isso compra 1.000 bananas, pois cada banana custa 1 euro.
Agora, a taxa de juro do empréstimo é de 5%, pelo que no final teria que devolver 1.050 euros, sendo os juros de 50 euros (1.000*5%).
Durante esse mesmo período de endividamento, vamos supor que a inflação esperada é de 2%. Portanto, as bananas já não custarão 1 euro, mas sim 1,02 euros cada.
O que acontece no final do período de financiamento? Se vendêssemos as bananas, ganharíamos 1.020 euros (1.000*0,02). Ou seja, o lucro seria de 20 euros. Mas, ao mesmo tempo, paguei juros de 50 euros. Portanto, em termos reais, o custo do empréstimo é de 30 euros (50-20).
Quanto valem esses 30 euros em bananas? Pois bem, dividimos 30 pelo preço final da banana (1,02 euros) resultando em 29,41 bananas. Então, para um empréstimo para comprar 1.000 bananas, pagamos 29,41 bananas. Isso significa que a taxa de juros real é de 29,41 em 1.000, o que equivale a 2,94% (29,41/1.000). Esta taxa é inferior à taxa de juro nominal (5%).
Podemos observar, portanto, que a equação de Fisher se cumpre, pois a taxa de juros nominal (5%) é igual (aproximadamente) à taxa de juros real (2,94%) mais a inflação (2%).
Outra maneira de expressar a equação de Fisher
Agora veremos outro exemplo para explicar como a equação de Fisher pode ser analisada sob outra perspectiva. Apresentaremos a situação do ponto de vista de um credor que chamaremos de Victoria. Ela tem 12 mil euros que pode poupar ou emprestar.
Se ela os emprestar, estará disposta a aceitar uma taxa de juros anual de 6%. Agora, a sua alternativa poderia ser comprar bens, por exemplo, cadeiras, e depois vendê-los a um preço mais elevado, o que dependerá da inflação.
Suponhamos que a inflação anual fosse de 4% e que Victoria emprestasse os 12.000 euros a 6% anuais. Qual foi o retorno real do empréstimo concedido?
Para calculá-lo, continuemos com o exemplo das cadeiras, para simplificar a análise. No momento da concessão do empréstimo, o seu preço era de 5 euros. Com a inflação (4%), subiu para 5,2 euros (5*1,04).
Agora calculamos a rentabilidade ou desempenho real de Victoria (1+r), como a de qualquer investimento, dividindo o valor final pelo investimento inicial.
O valor final é o valor emprestado acrescido de juros (1+i), mas expressamo-lo no número de cadeiras, dividindo pelo preço das cadeiras no final do prazo do empréstimo (5,2 euros), a que chamaremos de valor final preço ou ff. Temos o seguinte:
valor final = (1+i)/pf
Qual seria então o investimento inicial? Pois bem, para o exprimir, também em termos de número de cadeiras, devemos dividir o valor emprestado pelo preço do bem no momento 0, ou seja, 5 euros, a que chamaremos preço inicial ou pi.
Como nos preocupamos com o retorno de cada euro emprestado, dividimos apenas 1 por pi.
Investimento inicial 1/pi
A fórmula ficaria assim:

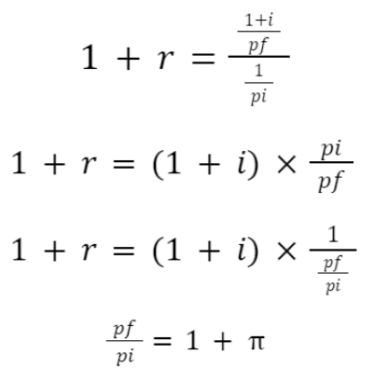
Portanto:
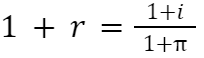
Tendo esta fórmula, voltando ao exemplo da Victoria, o retorno do empréstimo concedido é de:
- 1+r = (1+0,06)/(1+0,04) = 1,06/1,04
- 1+r = 1,0192
- r = 0,0192
- r = 1,92%
Podemos confirmar, novamente, que o juro ou rendimento real (1,92%) é inferior ao nominal (6%) e a diferença é dada pela inflação (4%).
Se prestarmos mais atenção, além disso, percebemos que se a taxa de inflação for superior à taxa de juro do empréstimo concedido, por exemplo, 8%, o retorno para Victoria é negativo.
- 1+r = (1+0,06)/(1+0,08) = 1,06/1,08 = 0,9815
- 1+r = 0,9815
- r = -0,0185
- r = -1,85%
Como esse resultado é explicado? Pois bem, acontece que teria sido melhor para Victoria, em vez de conceder o empréstimo, comprar cadeiras e depois vendê-las a um preço mais elevado.
As cadeiras já não passaram de 5 para 5,2 euros, mas para 5,4 euros. Assim, com os 12.000 euros que ia emprestar, compra 2.400 cadeiras (12.000/5) e depois vende-as por 5,4 euros cada, dando um total de 12.960 (2.400*5,4). O lucro foi de 960 euros (12.000-12.960). Por outro lado, se conceder o empréstimo, ganha apenas 6% sobre 12.000, ou seja, 720 (12.000*0,06).
Do exposto, podemos inferir que, se Victoria espera uma taxa de inflação mais elevada, também exigirá um juro nominal mais elevado para o empréstimo que irá conceder. Caso contrário, o seu desempenho será negativo. Isto explica, por outro ângulo, a relação entre as três variáveis que compõem a equação de Fisher.
Qual é a controvérsia em torno da fórmula de Irving Fisher?
Os analistas e colegas nem sempre concordam com a teoria, postulado ou fórmula dos seus colegas, como no caso de I.Fisher. No que diz respeito às finanças, a equação de Fisher permite explicar a taxa de juro nominal com base na taxa de juro real e na inflação.
Relativamente aos três conceitos que a sua equação unifica, a inflação e a taxa de juro real cujos resultados se situam fora da equação. Em caso de inflação pode depender de certas expectativas de inflação futura ou do défice fiscal.
No caso da taxa de juro real pode surgir de certas características institucionais ou mesmo de uma escolha das próprias pessoas na economia. Isto significa que, após a inflação e a taxa real serem definidas, a aplicação da equação de Fisher determinará o valor da taxa de juro nominal.
Uma coisa a esclarecer sobre a equação de Fisher é que ela não é a hipótese, embora a equação possa ser mencionada e a hipótese possa ser falada:
- A equação de Fisher, seria a prática e refere-se à solução matemática única do comportamento individual, mutuante ou mutuário, no que diz respeito à maximização do lucro.
- A hipótese de Fisher é a parte teórica que estabelece que a taxa real influencia a taxa nominal, embora não inversamente.
Isto significa que as variáveis reais afectam as variáveis nominais e não o contrário.
👉 Inflação | O que é, tipos e causas
O Efeito Fisher Internacional (FIE)
O Efeito Fisher International (FIE) é um modelo de taxa de câmbio pioneiro pelo economista Irving Fisher em 1930. Estabelece taxas de juro nominais atuais e futuras sem juros, excluindo a inflação pura.
Permite prever e compreender os movimentos presentes e futuros dos preços da moeda à vista. Para que o modelo EFI funcione correctamente, os elementos de capital sem risco têm de flutuar livremente entre países/estados com um par cambial específico.
Quais são as principais causas da inflação?
A inflação é o aumento geral e sustentado dos preços de bens e serviços dentro de uma economia, resultando na perda do poder de compra da população, tendo efeitos negativos na economia e nos indivíduos.
A inflação não é apenas o aumento dos preços e durante algum tempo, é um aumento contínuo dos preços, afectando a economia das pessoas e o funcionamento do mercado, as empresas de produtos e serviços, tendo de aumentar os seus preços de forma contínua e os salários dos trabalhadores sendo deixados para trás da inflação, perdendo o poder de compra.
A inflação é um círculo vicioso de aumento de custos, aumento de preços, aumento de salários. Isto impede que o mercado se mantenha estável.
Entre as principais causas da inflação, encontram-se as seguintes:
- Procura: À medida que a procura aumenta, o setor produtivo de diferentes produtos é esmagado pelo aumento, aumentando os preços.
- Custos: Quando os custos de produção aumentam, devido à desvalorização, crise económica ou outras razões, os produtores aumentam os seus preços de modo a não continuarem a perder lucros.
- Causas sociais ou inflação estrutural: quando há avisos sobre futuros aumentos de preços, os empresários podem decidir antecipá-los, aumentando os preços dos seus produtos.
Vantagens da Equação de Fisher
Previsibilidade eeconómica
A principal vantagem da Equação de Fisher é a sua capacidade de prever a relação entre a inflação e as taxas de juros. Investidores e formuladores de políticas utilizam esta relação para ajustar as suas expectativas em relação ao futuro, o que é crucial para a tomada de decisões económicas informadas.
Ferramenta de política monetária
A equação oferece aos bancos centrais uma estrutura para definir as taxas de juros de referência. Ao considerar a taxa de inflação esperada, os responsáveis pela política monetária podem estabelecer taxas de juros que visam estabilizar a moeda e controlar a inflação.
Simplicidade e clareza
A equação é apreciada pela sua simplicidade e clareza. Ela destila conceitos complexos numa forma que é facilmente compreensível e operacionalizável para economistas e profissionais do setor financeiro.
Desvantagens da Equação de Fisher
Expectativas de inflação
A maior limitação da Equação de Fisher é a sua dependência de expectativas de inflação, que são notoriamente difíceis de prever. As expectativas podem ser influenciadas por uma variedade de fatores, muitos dos quais são imprevisíveis ou baseados em sentimentos subjetivos.
Rigidez do modelo
A equação assume uma relação de um para um entre a taxa de juros nominal e a inflação esperada, o que pode não se materializar na realidade. O mercado financeiro é influenciado por uma gama complexa de variáveis, e a rigidez do modelo de Fisher pode não capturar a dinâmica completa do mercado.
Hipótese de racionalidade
A Equação de Fisher pressupõe que os agentes económicos têm expectativas racionais e agem com base na totalidade das informações disponíveis. No entanto, a teoria comportamental demonstra que os agentes frequentemente agem de maneira irracional ou estão sujeitos a vieses cognitivos.
Impacto de choques externos
A equação pode não ser eficaz em períodos de choques económicos severos ou eventos imprevistos (como crises financeiras ou pandemias), onde a relação entre as taxas de juros e a inflação pode se desviar significativamente das previsões da equação.
Em resumo, a Equação de Fisher oferece uma estrutura lógica para entender a relação entre juros e inflação, o que é extremamente valioso em economia e finanças. No entanto, a sua eficácia está limitada pela precisão das expectativas de inflação e pela suposição de que todos os agentes do mercado agem racionalmente. Essas limitações devem ser consideradas quando se utiliza a equação para informar decisões de política monetária ou investimentos financeiros.
- Ajudamos a encontrar s corretora certa para si
- Investigação independente, gratuita e não vinculativa
- Preencher este questionário em menos de 1 minuto
