Guia completo para a regressão linear múltipla

Neste artigo vamos ver o que é a regressão linear múltipla e para que serve, a sua fórmula, e como se calcula de forma simples. Para isso, vamos utilizar um exemplo prático com a ação da Apple.

O que é a regressão linear múltipla?

A regressão linear múltipla é uma extensão da regressão linear simples que permite examinar como múltiplas variáveis independentes estão relacionadas com uma variável dependente.

Seguindo com o exemplo dos gelados que vimos no artigo de regressão linear simples, onde vimos como a temperatura poderia afetar as vendas de gelados, vamos aprofundar mais e ver como outros fatores adicionais podem influenciar a mesma variável dependente.

Ou seja, poderíamos adicionar, por exemplo, o número de turistas para nos ajudar a explicar como se comporta em função de mais do que uma variável.

Fórmula da regressão linear múltipla

Seguindo com o nosso exemplo, além da temperatura (variável independente 1), poderíamos querer investigar como o número de turistas (variável independente 2) afeta as vendas de gelados (variável dependente).

A fórmula para um modelo de regressão múltipla é uma extensão do modelo de regressão linear simples:

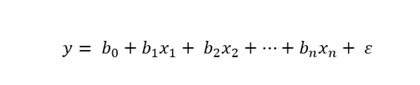
Por haver muitas variáveis e para simplificar, utiliza-se b para a beta (ou inclinação) e x para as variáveis independentes. Para identificá-las, adiciona-se um sub-índice que é o número que vê.

No nosso exemplo, a equação poderia ser:

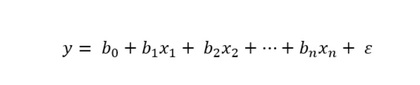
Onde:

• y: é o número de gelados vendidos:
• b0: é a interseção
• b1: é o coeficiente de variação de x1 (temperatura)
• b2: é o coeficiente de variação de x2 (número de turistas em milhares)
• e a espécie de E: que existe no final e é o erro.

Pense que quando fizermos o nosso cálculo isto nem sempre coincidirá com a realidade observada, pelo que a diferença entre a estimativa e a realidade é conhecida como erro ou resíduo, dependendo do contexto em que estamos a trabalhar.

E agora estará a perguntar-se: “e como se calcula isto?”

Como se calcula o modelo de regressão múltipla?

O processo de cálculo para a regressão múltipla é conceptualmente semelhante ao da regressão simples, mas matematicamente mais complexo devido à presença de múltiplas variáveis. Muitas vezes utiliza-se software estatístico avançado como R, Python ou até mesmo Excel para realizar estes cálculos.

1. Determinam-se as médias das variáveis dependentes e independentes.
   
2. Calculam-se as covariâncias e variâncias para cada par de variáveis independentes e a dependente.
   
3. Utilizam-se métodos como o de Mínimos Quadrados Ordinários (MQO) para estimar os coeficientes b que minimizam a soma dos quadrados dos resíduos (diferença entre valores observados e previstos).
   
4. Avalia-se a interseção e os coeficientes obtidos.

Dada a sua complexidade no cálculo, não entraremos em detalhes, mas como dissemos anteriormente, a essência é a mesma e pode ser calculada com qualquer software estatístico como R e Excel ou até mesmo utilizando bibliotecas estatísticas em Python.

Como se interpreta um modelo de regressão múltipla?

Isso sim, muito mais importante que os detalhes do cálculo matemático, é a interpretação. Suponhamos que depois de calcular o nosso modelo de venda de gelados diários segundo a temperatura e segundo o número de turistas (em milhares) que visitaram a cidade nesse dia, temos o seguinte:

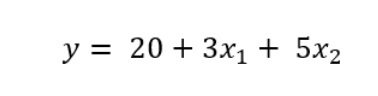
Isso significa que, segundo o nosso modelo, se um dia não houvesse nem temperatura nem turistas, vender-se-iam 20 gelados (o que é uma situação pouco realista e serve apenas para completar o modelo matemático). Por cada grau que aumenta a temperatura, vendem-se 3 gelados adicionais, e por cada mil turistas adicionais que visitam a cidade, vendem-se 5 gelados adicionais.

Agora, imagina que queremos prever quantos gelados se venderiam num dia que faz 30 graus e visitaram a cidade 20.000 turistas.

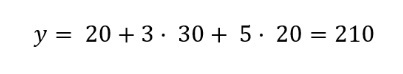
A nossa previsão nessas condições é que se venderão 210 gelados nesse dia.

Agora bem, é vital destacar que estes coeficientes apresentam suposições que assumimos previamente. A interpretação está baseada na suposição de que as outras variáveis permanecem constantes, o que raramente ocorre na vida real. Por exemplo, um aumento na temperatura poderia também atrair mais turistas, e este modelo simplificado não captura essa interação entre as variáveis independentes.

Como fazer uma regressão linear múltipla aplicada ao trading? | Exemplo prático

No mundo do trading, a regressão múltipla é utilizada habitualmente para analisar como diferentes fatores económicos, assim como bolsistas, afetam o preço de um ativo. Por exemplo, suponhamos que queremos investigar como o preço das ações da Apple está influenciado pela venda de smartphones a nível global, o investimento em I&D da companhia e a taxa de câmbio EUR/USD.

A primeira coisa que devemos verificar sempre é se as variáveis que vamos utilizar fazem sentido, então vamos a isso:

• Vendas globais de smartphones (x1): Representa a procura global de smartphones, que pode influenciar diretamente nas receitas da Apple. Mediremos em centenas de milhões de vendas. De modo que se o valor for 1, na realidade significará que foram vendidos 100 milhões, se o valor for 10, então 1.000 milhões.

• Investimento em I&D (x2): Indica quanto a Apple está a investir em investigação e desenvolvimento, o que pode afetar a sua inovação e, por conseguinte, o seu valor no mercado. Uma unidade será igual a 1.000 milhões.

Uma vez explicadas as variáveis, teremos uma equação como a seguinte:

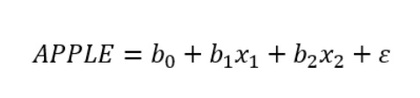
Onde:

• APPLE é o preço das ações da Apple
• b0 é a interseção
• b1, b2 são os coeficientes para cada uma das variáveis descritas anteriormente.
• E é o erro

Com isto em mente, extraímos os dados, utilizamos o nosso software de cálculo estatístico e obtemos o seguinte:

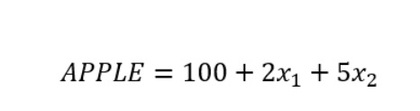
Como se interpreta?

E bem, como se interpreta isto? Vamos a isso:

• Por cada 100 milhões vendidos nas vendas globais de smartphones, o preço das ações da Apple aumenta em 2 dólares.
• Por cada 1.000 milhões adicionais que a Apple investe em I&D, o preço das ações aumenta em 5 dólares.

Agora, imaginemos que estes dados são verdadeiros. Segundo os dados, a Apple investiu em 2022, a quantia de 26.000 milhões em I&D e foram vendidos 1.200 milhões de smartphones a nível global.

Se aplicarmos isto à equação, teríamos que:

Apple=100+(2·12)+(5·6)=254€/ação

Lembre-se que multiplicamos por 12, porque cada unidade equivale a 100 milhões. Ao vender-se 1.200 milhões, temos que multiplicar por 12. Algo semelhante ocorre no investimento em I&D, cada unidade equivale a 1.000 milhões, pelo que ao ser 26.000 milhões, devemos multiplicar por 26.

O resultado é que, segundo esta estimativa, as ações da Apple deveriam ter um preço aproximado de 254 dólares por ação. Aqui tens um gráfico em 3D de como mudaria o preço segundo cada variável.

Para que serve a regressão linear múltipla?

A regressão linear múltipla é uma ferramenta estatística poderosa com uma ampla gama de aplicações em diversos campos. Em geral, serve para vários propósitos chave:

1. Previsão: Permite estimar e prever o valor de uma variável dependente com base nas variações de duas ou mais variáveis independentes. Este modelo pode prever resultados futuros a partir de dados existentes, o que é essencial em áreas como a meteorologia, o planeamento financeiro e a gestão de recursos.
   
2. Inferência causal: Ajuda a entender as relações entre variáveis e a determinar o impacto de uma ou mais variáveis independentes sobre uma variável dependente. Isto é crucial em campos como a economia, a sociologia e a ciência política, onde os investigadores estão interessados em efeitos causais.
   
3. Controlo de variáveis confusas: Em estudos onde múltiplos fatores influenciam o resultado, a regressão linear múltipla permite isolar o efeito de uma variável ajustando por outras. Isto é importante em estudos médicos e sociais, onde variáveis confundentes podem distorcer as relações verdadeiras.
   
4. Otimização de processos: Em engenharia e manufatura, a regressão pode ser utilizada para otimizar processos ao entender como várias variáveis afetam um resultado de qualidade ou eficiência.

Aplicação no Trading

No âmbito do trading, a regressão linear múltipla é utilizada para vários propósitos estratégicos e analíticos:

1. Modelação de preços de ativos: Os traders podem utilizar a regressão para modelar como diversos fatores económicos, financeiros e de mercado afetam os preços dos ativos. Por exemplo, o preço de uma ação poderia depender de variáveis como as taxas de juro, o desempenho do setor e indicadores económicos gerais.
   
2. Desenvolvimento de estratégias de trading quantitativo: Os modelos de regressão podem ajudar a identificar relações lineares entre diferentes ativos financeiros (como ações e obrigações) e utilizar essas relações para desenvolver estratégias de trading algorítmicas. Por exemplo, um modelo poderia indicar que certas combinações de variáveis indicam um momento ótimo para comprar ou vender um ativo.
   
   Desta forma, uma vez detetada a estratégia, poderíamos aplicá-la com um bot de sistema, ligado à API KEY da corretora, para colocá-la a funcionar de forma autónoma num processo chamado trading automático.

Em suma, a regressão linear múltipla serve-nos para descobrir, ou pelo menos estimar como se comportará uma variável que queremos conhecer, com base noutras variáveis das quais depende. E claro, estes modelos matemáticos têm muitas aplicações práticas – tecnologia, medicina, e claro, trading.